Escribo esto pocos días después de un eclipse anular de Sol que pasó por el sur de Argentina. Desde Buenos Aires no se pudo ver mucho pero la iluminación disminuyó considerablemente y en las sombras de las hojas de los árboles se podía ver el Sol tapado. Pero a pesar de que se puede argumentar que el espectáculo fue peor que en el pueblito de Facundo, donde fue el máximo, me permitió medir la distancia entre la Tierra y la Luna usando sólo una fotografía.

Un eclipse solar se produce cuando la Luna se alinea con la Tierra y el Sol. Como la Luna es 400 veces más chica que el Sol (en diámetro) pero está 400 veces más cerca, sus tamaños aparentes son muy parecidos, dando lugar a que ésta tape todo el disco solar. En el caso de los eclipses anulares la Luna se encuentra un poco más lejos de la Tierra, haciendo que no logre tapar todo y se pueda observar un anillo.

Si cierran un ojo y ponen un dedo adelante de su cara tapando un objeto lejano y luego cambian de ojo, el objeto deja de estar tapado. Lo mismo pasa en un eclipse. Ese movimiento aparente del dedo con respecto a los objetos lejanos es lo que se llama paralaje y sucede lo mismo con la Luna. Desde Buenos Aires, la Luna y el Sol no estaban alineados y ésta tapó sólo una parte.

Y esta es la foto que vamos a usar para estimar la distancia a la Luna. ¿Cómo? Usando un poco de geometría. A partir de la foto se puede estimar el paralaje de la Luna y, sabiendo la distancia entre Facundo y Buenos Aires, conseguir la distancia entre la superficie de la Tierra y la Luna.

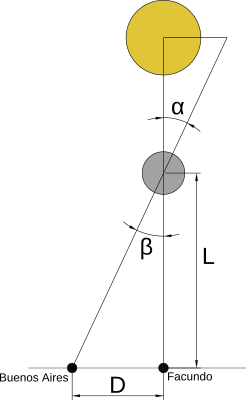
En este esquema se ignora la curvatura de la Tierra y se supone que la alineación perfecta se dio en Facundo al momento del máximo. Ambas son aproximaciones bastante groseras. Además, también asume que el máximo se dio al mediodía, lo cual es totalmente falso y hace que nuestro cálculo sea una subestimación importante.

La foto está sacada en un ángulo, por lo que hay problemas de perspectiva. Estos los podemos minimizar estirando la imagen. Si a la imagen modificada le superponemos dos círculos representando el Sol y la Luna, podemos calcular la distancia (en pixels) entre sus centros:

Pero la separación en pixels no nos dice nada si no sabemos qué ángulo representa. Sabiendo que el disco solar cubre 0,53° del cielo y contando cuántos pixels representan en la imagen, se puede saber el ángulo de paralaje con un poco de regla de tres simple (que me dio unos 0,34° 0,17°). Luego, considerando que la distancia entre Facundo y Buenos Aires es de 1.544 km se puede calcular la distancia a la Luna como

El cálculo del paralaje da la distancia entre el centro de la Luna y la superficie de la Tierra. Para tener la distancia entre ambos centros hay que sumar el radio de la Tierra (6.371 km).

La distancia real a la Luna, medida con lásers que se reflejan en espejos dejados allí por el programa Apollo es de de 384,400 km. El error es del orden de 40%, lo cual no es muy bueno, pero satisfactorio si se tiene en cuenta todas las múltiples fuentes de error y demuestra que se puede medir la distancia a los astros sin gastar 110 mil millones de dólares en mandar humanos hasta ahí.

Actualización

Un lector me hizo notar que el cálculo del ángulo de paralaje estaba mal. La corrección hace que la medición sea una sobreestimación (aunque el orden del error es casi idéntico). Si se hace un modelo más realista, teniendo en cuenta la curvatura de la Tierra y la altura a la que estaba el Sol sobre el horizonte, se llega a una distancia de 241.000 km (el cálculo analítico es medio tedioso, así que yo hice algo muy cavernícola y simplemente dibujé el esquema con las medidas reales en AutoCAD y medí la distancia). El resultado es una subestimación y sigue siendo con un 40% de error, aproximadamente.

Esto demuestra, me parece, que el problema principal no es el modelo que estamos usando sino que la medición del ángulo no es muy buena ni tampoco la suposición de que fue tomada precisamente en el momento del máximo. Haciendo el mismo ejercicio cavernícola con AutoCAD usando la distancia correcta a la Luna, da que el paralaje esperado es más bien de 0.10°. Considerando la mala calidad de la imagen (especialmente los problemas con la perspectiva) no creo que pueda usarse para medir el ángulo con tanta precisión.

No se preocupen, en el próximo eclipse voy a tratar de hacerlo mejor.